Math can be hard and frustrating for students with dyscalculia, but with the right scaffolds and support, it doesn’t have to be. Many strategies can be implemented to help students with dyscalculia. But first, what is dyscalculia?
What is Dyscalculia?
Dyscalculia is a specific learning disability. Students with dyscalculia have persistent difficulties in understanding and using mathematical concepts, symbols, and relationships. It has nothing to do with effort from the student. Dyscalculia is related to difficulties in processing numerical information.

Math can be hard and frustrating, but with the right scaffolds and support, it doesn’t have to be. Many strategies can be implemented to help students with dyscalculia. But first, what is dyscalculia?
Understanding Dyscalculia
Dyscalculia is a specific learning disability. Students with dyscalculia have persistent difficulties in understanding and using mathematical concepts, symbols, and relationships. It has nothing to do with effort from the student. Dyscalculia is related to difficulties in processing numerical information.
So, what interventions can you implement daily? Here are 10 strategies that will get your students to make progress.
7 Strategies to Help Students with Dyscalculia
#1 Utilizing Tactile Learning: Math Manipulatives for Dyscalculic Students
Students with dyscalculia struggle with the relationship between numbers. So make it attainable with manipulatives. Students need to learn math in a tactile way to make the math understandable.
Try using a DIY meter tape so students have an understanding of place value and fraction decimla equivalency.


Use DIY meter tape to teach students how to round decimals and to teach place value, which you can get HERE.

Another example is to use base tens blocks to learn how to add, subtract, multiply, and divide.

#2 Visual Aids: A Necessity for Dyscalculic Students
Visual aids are a must for students with dyscalculia. Whenever possible, use them when you are introducing a concept. Once your student has mastered solving the equation with visual models, replace the visuals with numbers.
Draw Base tens blocks
Once your students have had experience touching and moving base ten blocks, it is time to draw them when solving equations. They can be drawn to add, subtract, multiply, and divide.
Here is a strategy I use to teach students how to perform long division using the area model or box method. I wrote a blog post on how I teach students how to divide with the area/box method.
Students with dyscalculia are capable of solving these problems with guidance, and they will have success with dividing numbers using visuals.
Visual Models of Fractions
Visual models are non-negotiable when learning how to add, subtract, multiply, and divide fractions with students with dyscalculia. But which ones should you use? Number lines or area models?
Don’t use number lines with students with dyscalculia unless the number lines are already labeled. If you ask your students to draw a number line, that is just one extra step that you are asking them to do.
Teach your students how to add and subtract unlike fractions by drawing them. I explain how to teach adding and subtracting unlike fractions in this blog post.
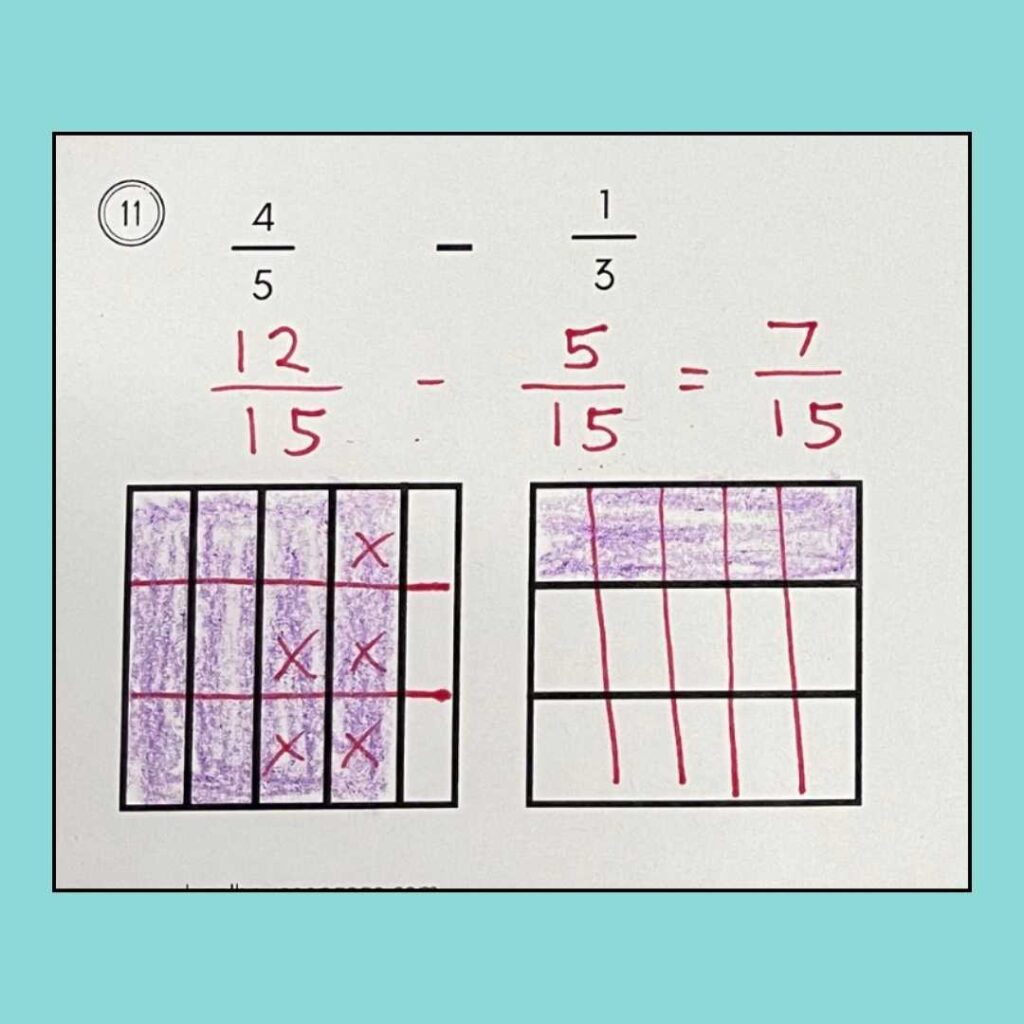
Check out my visual model resource for adding and subtracting unlike fractions by clicking HERE

#3 Mnemonics: Memory Aids for Dyscalculia
Mnemonics are a great way to help your student with dyscalculia remember some of the steps to solving problems. For specific mnemonic ideas to use with upper-elementary students, read my 13 Math Mnemonics to Use in 5th Grade blog post.
#4 Adapting Curriculum: Modifying Problems for Dyscalculic Students
Modifying problems is a must! I teach my dyscalculia students grade-level curriculum because they need the exposure, but I modify it by using simple problems.
Use Simple Fractions
Use numbers below 10 when teaching how to add and subtract fractions with unlike denominators when first introducing steps to solve this type of problem.
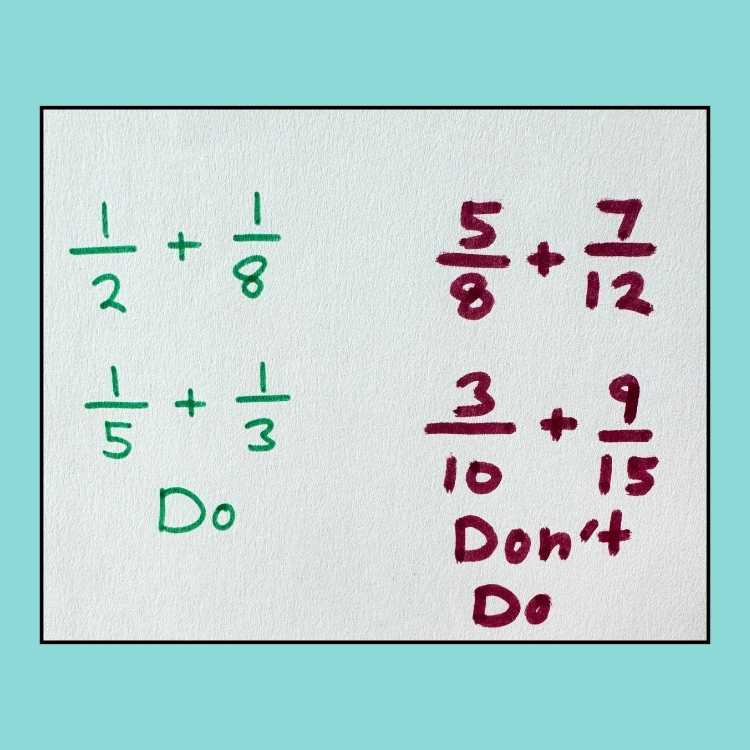
Add and Subtract Whole Numbers Without Regrouping
Use problems with only 3 or 4 digits (depending on the level of the student) that do not require regrouping (or borrowing).
Use Decimals Only to Hundredths
Use decimals that have the same place value when solving addition and subtraction problems. Instead of 1.09 – 0.7, give problems like 1.09 – 0.07 so that it is easy for students to line up the decimals.
Multiply decimals with whole numbers
Use problems that only go up to hundredths and don’t include problems with thousandths until they show mastery.
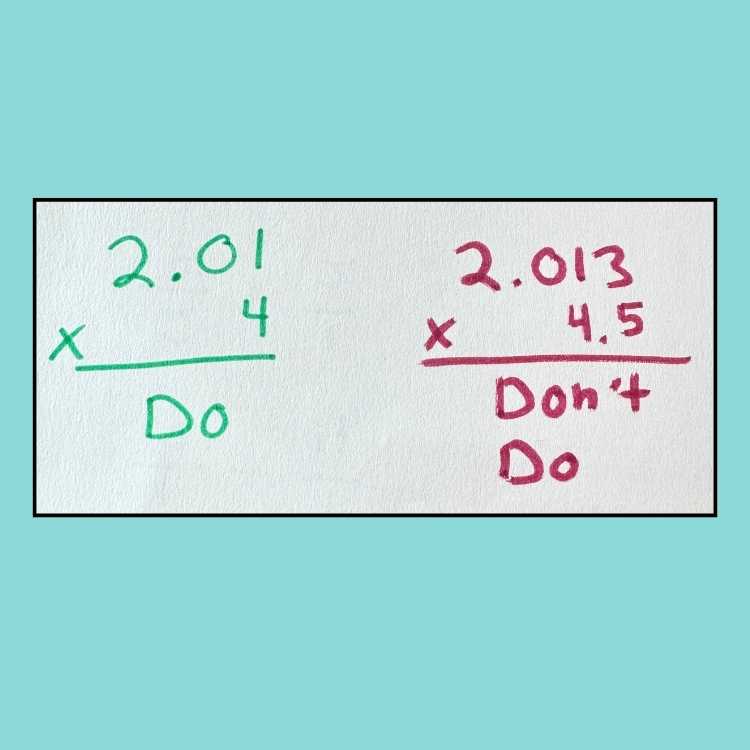
#5 Color Code: Visual Organization for Dyscalculic Students
Color-code different problems on the board so they don’t look all mixed up. If I’m showing examples of how to solve problems using different methods, I will make each problem a different color.

#6 Improve Math Understanding Through Patterns
Math is all about patterns. The rules stay the same, but the numbers change. Support your dyscalculia students by asking them to look for patterns.
Patterns in Simplifying Fractions
Ask students to find the patterns when simplifying fractions so that they can see the different methods.
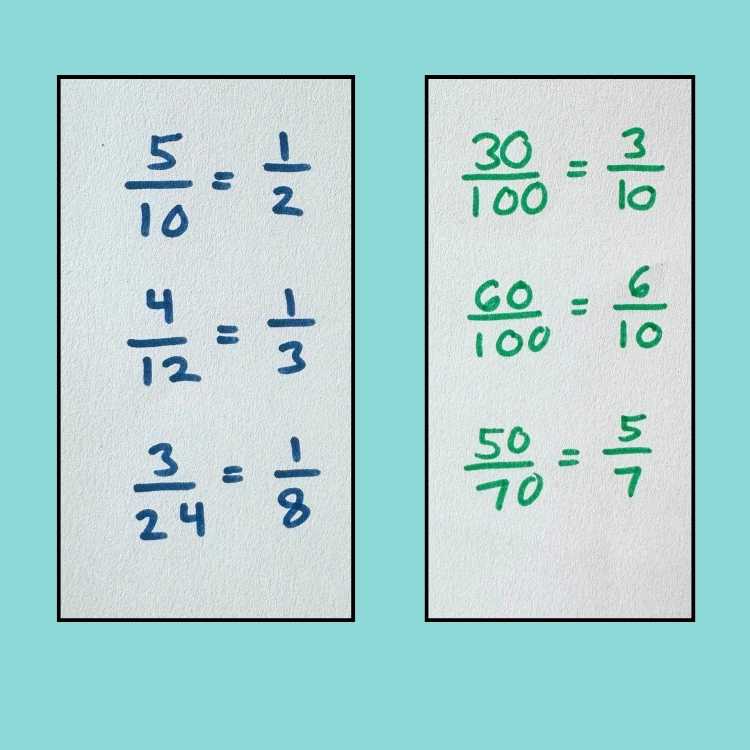
The fractions in blue were simplified by dividing using the numerator, and the fractions in green used 10 as the divisor.
There are other ways, of course, to simplify a fraction, but with a student who is struggling in math already, only show them two ways of doing it. Keep things simple!
Patterns in Multiplying Fractions with a Whole Number
Show your students examples of how to find a fraction of a whole number using a tape diagram. Ask them what patterns they see.

#7 Break Down Problems: Incremental Learning for Dyscalculia
Math equations involve a lot of steps in grade 5. Break down problems into small steps by just focusing on one aspect of the problem per day and gradually increasing the difficulty.
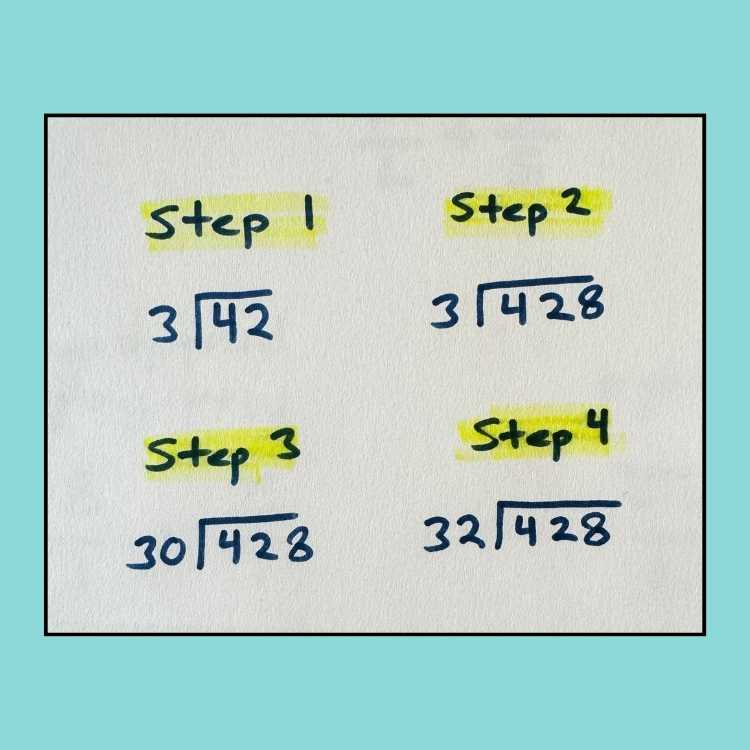
For example, when teaching long division, start with problems that have a two-digit dividend and a one-digit divisor, like 42/ 3. Once they have mastered that, move on to a 3-digit dividend like 428/3. Use a gradual increase in difficulty.
Final Thoughts
These strategies can support students with dyscalculia in upper grades. Whether you decide to use tactile learning tools or mnemonic devices , you will be creating an inclusive learning environment.
For more ways you can help students who are below grade level in math, be sure to read: How to Help Struggling Math Students in 5th Grade . You got this! Giselle
Save this post for later. Click on the image below to save it to your teacher’s Pinterest board. 📌📌📌



